In the field of computer vision, one of the main issues is how exactly we recover 3D shape of a target object from its perspective images. Several methods for estimating camera motion and reconstructing 3D shape have been proposed such as shape from X(X:shading,texture,contour and motion). These methods have been useful in many fields such as virtual reality, shape recognition, navigation for a moving robot, virtual city space and commercial advertisements on web sites. However those methods have difficulties of being highly sensitive to noise. To overcome these problems, we propose a fusion method of 3D shape obtained from multiple view points. First, 2D point correspondence is supplied to make the 3D shape. We propose an automatic point correspondence method based on the Kanade-Lucas feature point tracking method. Second, deciding the 2D point correspondence, we recover 3D shapes in the same view point set by using Mukai's method. The same view point set means that there is no self occlusion among the shapes in the same view point set. Then, we fuse 3D shapes which are the same shapes but in the different coordinate system due to camera movement. We regard this part as the partial shape fusion process. Finally, we consider the self occlusion. By integrating 3D partial shapes obtained from the partial shape fusion process and selecting the high accuracy points in each partial shape, the whole shape can be obtained with high accuracy.
2. Improving the Point Correspondence Accuracy of Kanade-Lucas Method by Affine Transformation and Correlation
The Kanade-Lucas(KL) feature tracker is one of the good matching methods. However it fails to find corresponded points of two images when image motion is large. We propose a feature point matching method by using affine transformation and correlation so that KL method works well for large image motion. First, KL method is used to match points. Some points are matched well, other points are mismatched or failed to be matched. Second, correlation of two matched points between the first and the second images obtained by KL method is used to discriminate well matched point and badly matched point. If correlation coefficient is lower than a specified threshold, it is regarded as an outlier. Third, all the points to be matched in the first image are transformed on the second image by affine transformation obtained by using well matched points alone. However, all the transformed points from the first image to the second image are not matched well due to the approximation of camera movement by affine transformation. The role of affine transformation is to reduce the computation time and the number of mismatching points by designating only the small searching area around the transformed point. Finally, correlation is used to find the best matching point around the transformed point. Real image has been used to test the proposed method, and excellent results have been obtained with the error of 0.811 pixels in average(Fig.1).


Fig.1 Experimental images. (a) is the first image. (b) is the second image. 28 reference points(white dots) in the first image are required to be tracked in the second image.
3. Fusion of 3D Shapes in Multiple View Points to Obtain More Accurate Shape
The aim of this section is to obtain an exact 3D model using multiple images captured by a camera in the same viewpoint set. The reconstruction of 3D shape using two images has problems such as being weak at noise. Therefore we present a method to reduce noise and to improve the accuracy of 3D shape with multiple images. The method consists of three stages: firstly, reconstruction of 3D shapes at different camera positions, secondly fusing the 3D shapes to obtain a para-ideal shape, and thirdly removing the outlier shapes and feature points by evaluation function, and fusing the rest of shapes. Even though the corruption of image data by noise is one of the unavoidable problems in any system, noise is removed effectively by the proposed method in multiple view points. Experimental results show that our system performs well to remove noise with robustness. The maximum noise reduction rate is 82% in the real image experiment(Fig.2).
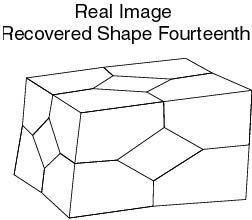
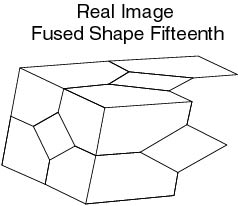
Fig.2 Left shape: reconstructed shape without fusion method. Right shape: fused shape. There are lost three points in the shapes as outliers.
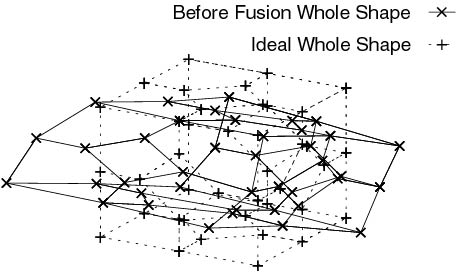
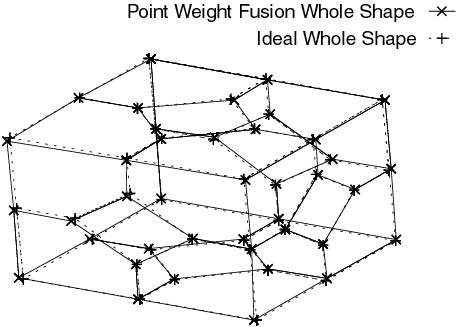
4. Recovery of 3D Whole Shape and Accuracy Improvement by Fusing Partial Shapes
In this section, we describe a novel approach for recovering an exact 3D whole model using image sequences. To recover a whole shape, more than two shapes in the different view point sets should be used, which is convenient to avoid problems such as inclusion of noise and self occlusion. We present a method of fusion and integration of 3D shapes. The fusion process indicates that 3D partial shapes in the same viewpoint set are fused sequentially to improve accuracy. The integration process indicates that refined partial shapes by the fusion process in each viewpoint set are integrated to construct the whole shape with high accuracy. A novel iterative orthonormal fitting transform method(IOFTM) is proposed to transform the shapes' coordinate system to the standard one. IOFTM is compared with the steepest descent method. We fuse shapes by the point-weighted fusion method. The whole shape is constructed by the integration of partial shapes' points which are at lower noise level between corresponding feature points. The method consists of five stages: first, reconstruction of partial shapes at different camera positions, second, fusion of the partial shapes to obtain a para-ideal shape by the uniform-weighted fusion method, third, detection of the outlier shapes and feature points based on an evaluation function, fourth, fusion of shapes by the point-weighted fusion method, and fifth, integration of accurate partial shapes to construct the refined whole shape. Experimental results indicate that our system performs well in removing noise with robustness. The noise reduction rates are 85.8% - 97.4% in the simulation and real image experiments, respectively(Fig.3).